Lecture 5 - 2025 / 3 / 3

Monotone circuits for the majority function

Definition (Boolean circuit): f:{0,1}n→{0,1}f : \{0, 1\}^n \to \{0, 1\}，通过门进行计算，每个门即 {0,1}2→{0,1}\{0, 1\}^2 \to \{0, 1\} 的函数（共 1616 种门）。

Claim: 几乎所有 nn 个输入的 Boolean function 需要 2nn\dfrac{2^n}{n} 个门（包括输入门）。

首先 nn 个输入的 Boolean function 有 22n2^{2^{n}} 种。

考虑 SS 个门能够表达多少种 Boolean function。首先每个门可以选择 S2S^2 种输入，以及自身有 1616 种计算方法，故函数数量不超过
(16S2)S(16S^2)^S

将 SS 用 2nn\dfrac{2^n}{n} 带入，由于
Sln⁡(16S2)=2nnln⁡(16⋅4nn2)=2nn(ln⁡16+nln⁡4−2ln⁡n)=2nln⁡4+⋯S\ln (16 S^2) = \frac{2^n}{n} \ln(16 \cdot \frac{4^n}{n^2}) = \frac{2^n}{n} (\ln 16 + n\ln 4 - 2 \ln n) \\ = 2^n \ln 4 + \cdots

另一方面
ln⁡22n=2nln⁡2\ln 2^{2^n} = 2^n \ln 2

从而 S<2nnS < \dfrac{2^n}{n} 时，lim⁡n→∞(16S2)S22n=0\lim\limits_{n \to \infty} \dfrac{(16 S^2)^S}{2^{2^n}} = 0。

Definition (monotone circuits): 一个电路是单调的，当且仅当它的所有门都是单调函数，即：
f(x1,⋯ ,xn)=1,∀i,yi≥xi⇒f(y1,⋯ ,yn)=1f(x_1, \cdots, x_n) = 1, \forall i, y_i \ge x_i \Rightarrow f(y_1, \cdots, y_n) = 1

现在考虑众数函数 Majn(x1,⋯ ,xn)\text{Maj}_n(x_1, \cdots, x_n)，试图找到一个单调电路来实现它。

一个最优的实现 Maj3\text{Maj}_3 的电路为（因为只用到了单调的 ∧,∨\land, \lor，故这个电路也是单调的）：
(x1∧(x2∨x3))∨(x2∧x3)(x_1 \land (x_2 \lor x_3)) \lor (x_2 \land x_3)

Theorem: 存在一个单调电路计算 Majn\text{Maj}_n，nn 为奇数，门的数量是 poly(n)\text{poly}(n)，深度是 O(log⁡n)O(\log n)。

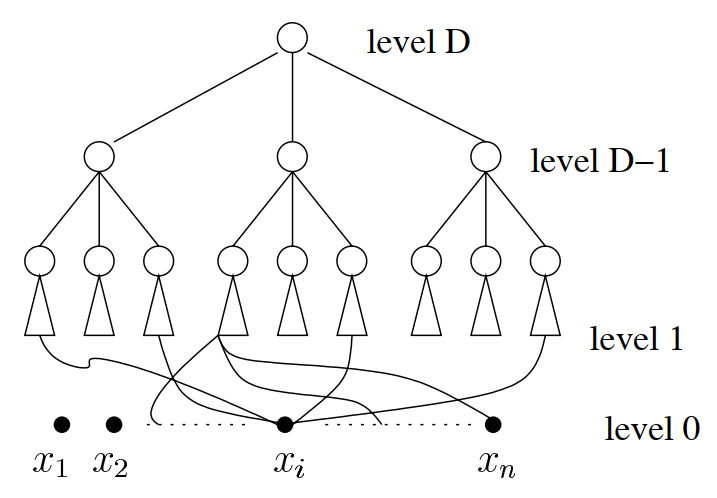
考虑一个随机电路 CC，包含 D=O(log⁡n)D = O(\log n) 层的 Maj3\text{Maj}_3，底层每个 Maj3\text{Maj}_3 随机从 x1,⋯ ,xnx_1, \cdots, x_n 中选择 33 个输入。

不妨设众数为 11，那么底层每个门输入 11 的概率至少为 p0=n+12n=12+12np_0 = \dfrac{n+1}{2n} = \dfrac{1}{2} + \dfrac{1}{2n}。

如果一个 Maj3\text{Maj}_3 的每个输入有 pp 的概率为 11，那么其输出为 11 的概率为
f(p)=p3+3p2(1−p)=3p2−2p3f(p) = p^3 + 3p^2(1-p) = 3p^2 - 2p^3

考虑迭代过程 p1=f(p0),p2=f(p1),⋯p_1 = f(p_0), p_2 = f(p_1),\cdots，目标为证明在 O(log⁡n)O(\log n) 次迭代后，p≥1−2−(n+1)p \ge 1 - 2^{-(n+1)}，从而根据 union bound，Pr⁡[∃x,C(x)≠Majn(x)]≤2n⋅2−(n+1)=12\Pr[\exists \bm x, C(\bm x) \ne \text{Maj}_n(\bm x) ] \le 2^n \cdot 2^{-(n+1)} = \dfrac 1 2，根据概率方法立刻得证。

  1. 第一阶段，12+12n≤pt≤34\dfrac{1}{2} + \dfrac{1}{2n} \le p_t \le \dfrac 3 4，由于步长增大，计算得
    (pt+1−12)≥118(pt−12)\left(p_{t+1} - \dfrac{1}{2} \right) \ge \dfrac{11}{8} \left (p_{t} - \dfrac{1}{2} \right)

    故在 O(log⁡n)O(\log n) 步内，ptp_t 可以达到 34\dfrac{3}{4}。

  2. 第二阶段：pt≥34p_t \ge \dfrac{3}{4}，设第一次达到这个要求为 pt0p_{t_0}，则：
    (1−pt+1)≤3(1−pt)2≤3(1−pt0)2t+1−t0≤342t+1−t0(1 - p_{t + 1}) \le 3 (1 - p_t)^2 \le 3 (1 - p_{t_0})^{2^{t+1-t_0}} \le \dfrac{3}{4^{2^{t+1 - t_0}}}

    故在 O(log⁡n)O(\log n) 步内，ptp_t 可以达到 1−12n+11 - \dfrac{1}{2^{n+1}}。

从而总共只需 D=O(log⁡n)D = O(\log n) 次迭代即可。