Lecture 4 - 2025 / 2 / 27

Unbalancing lights

对于 n×nn\times n 的灯泡矩阵，每行、每列各有一个开关，作用是翻转完整的一行、一列。

现在对于一个初始状态，试图通过操作开关最大化亮灯数。

Claim: 对于每一种初始状态，存在操作方式使亮灯数量当 n→∞n\to \infty 时渐进 n22+12πn3/2\dfrac{n^2}{2} + \sqrt{\dfrac{1}{2\pi}} n^{3/2}

首先均匀随机操作每一列的开关。用 Xij=±1X_{ij} = \pm 1 表示 (i,j)(i, j) 位置的灯是否亮。

对于第 ii 行，用 Zi=∑jXijZ_i = \sum_j X_{ij}，由于 Xi1,⋯ ,XinX_{i1}, \cdots, X_{in} 在 {1,−1}\{1, -1\} 中均匀随机，因此由随机游走结论：E[∣Zi∣]∼2πn\mathbb E[|Z_i|] \sim \sqrt{\dfrac{2}{\pi}n}

对于每一行的开关，如果操作后亮灯数量增多就操作它。从而根据期望的线性性：E[#on−#off]∼2πn3/2\mathbb E[\text{\#on} - \text{\#off}] \sim \sqrt{\dfrac{2}{\pi}} n^{3/2}

从而 E[#on]∼n22+12πn3/2\mathbb E[\text{\#on}] \sim \dfrac{n^2}{2} + \sqrt{\dfrac{1}{2\pi}} n^{3/2}。

Large girth and chromatic number

Definition (girth): 一个图 GG 的周长为其中最小环的长度。

Definition (chromatic number): 一个图 GG 的染色数为同色不相邻染色，最少需要的颜色数。

Theorem: ∀k,l\forall k, l，存在一张图的周长 ≥l\ge l，染色数 ≥k\ge k。

取随机图 G∼Gn,pG \sim \mathcal G_{n, p}，这里 p=n−1+1/lp = n^{-1 + 1 / l}。

用 XX 表示 GG 的 <l< l 的环数量，YY 表示最大独立集的大小。

首先 E[X]=∑i=3l−1ni‾2ipi≤∑i=3l−1(np)i2i=∑i=3l−1ni/l2i=O(n1−1/l)=o(n)\mathbb E[X] = \sum_{i=3}^{l-1} \dfrac{n^{\underline i}}{2i} p^i \le \sum_{i=3}^{l-1} \dfrac{(np)^{i}}{2i} = \sum_{i=3}^{l-1} \dfrac{n^{i/l}}{2i} = O(n^{1 - 1/l}) = o(n)

从而 Pr⁡[X≥n2]=o(1)\Pr[X \ge \dfrac{n}{2}] = o(1)。

另一方面，任取 yy，
Pr⁡[Y≥y]≤(ny)(1−p)(y2)≤ny⋅e−p(y2)≤(eln⁡n−py/4)y\begin{aligned} \Pr[Y \ge y] & \le \binom{n}{y} (1-p)^{\binom{y}{2}} \\ & \le n^y \cdot e^{-p \binom{y}{2}} \le (e^{\ln n -p y/4})^y \end{aligned}

取 y=8ln⁡np=8ln⁡n⋅n1−1/l=o(n)y = \dfrac{8\ln n}{p} = 8 \ln n \cdot n^{1 - 1/l} =o(n)，就有 Pr⁡[Y≥y]≤e−ln⁡n⋅y=o(1)\Pr[Y \ge y] \le e^{-\ln n\cdot y} = o(1)。

因此，根据 union bound，当 nn 足够大，GG 有 ≥12\ge \dfrac 1 2 的概率满足：

从每个环中删去一个点，剩下的图 G′G' 周长 ≥l\ge l，染色数 ≥ny=ω(1)\ge \dfrac{n}{y} = \omega(1)，从而 nn 充分大一定可以满足染色数 ≥k\ge k。

MAX3SAT

记 φ={(x1∨¬x2∨x3),⋯ }\varphi = \{ (x_1 \lor \neg x_2 \lor x_3), \cdots \}，其中的每一项称为一个 clause。

Claim: 对于任一个 φ\varphi，存在一种赋值方法使至少 78∣φ∣\dfrac 7 8 |\varphi| 的 clause 被满足。并且可以高效找出。

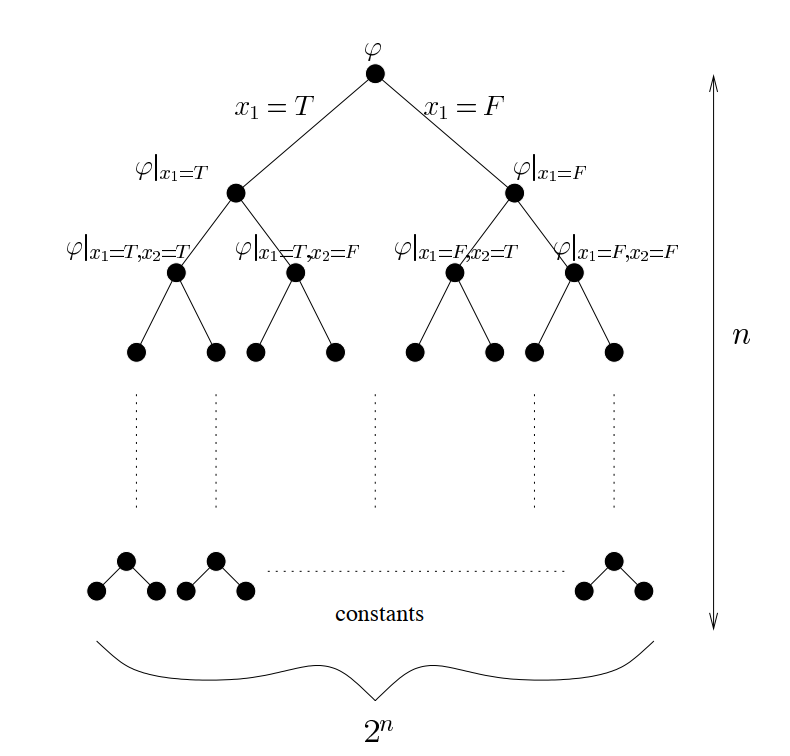
存在性只需要随机赋值即可证明。

依次考虑每一个 xix_i，由于 78∣φ∣=E[φ]=Pr⁡[x1=T]⋅E[φ∣x1=T]+Pr⁡[x1=F]⋅E[φ∣x1=F]\dfrac 7 8 |\varphi| = \mathbb E[\varphi] = \Pr[x_1 = T] \cdot \mathbb E[\varphi | x_1 = T] + \Pr[x_1 = F] \cdot \mathbb E[\varphi | x_1 = F]

从而一定能有一种条件期望 ≥78∣φ∣\ge \dfrac 7 8 |\varphi|，递归下去寻找即可。

这种方法叫做 Method of conditional probabilities。

4-Cliques / Triangles

Definition (threshold): 称 p(n)p(n) 是性质 QQ 的 threshold，当且仅当：
p≫p(n)  ⟹  Pr⁡[G∈Gn,p has Q]→1 as n→∞p≪p(n)  ⟹  Pr⁡[G∈Gn,p has Q]→0 as n→∞p \gg p(n) \implies \Pr[G \in \mathcal{G}_{n,p} \text{ has } Q] \to 1 \text{ as } n \to \infty \\ p \ll p(n) \implies \Pr[G \in \mathcal{G}_{n,p} \text{ has } Q] \to 0 \text{ as } n \to \infty

对于图 G∼Gn,pG \sim \mathcal{G}_{n,p}，设 XX 为其中的 4-Clique 的个数，XC=0/1X_C = 0/1 代表 CC 是不是 4-Clique。
E[X]=(n4)p6=Θ(n4p6)\mathbb E[X] = \binom{n}{4} p^6 = \Theta(n^4p^6)

Theorem: p(n)=n−2/3p(n) = n^{-2/3} 是包含 4-Clique 的 threshold。

首先 p≪p(n)p \ll p(n) 时，由于 E[X]→0\mathbb E[X] \to 0，因此 Pr⁡[X≥1]≤E[X]→0\Pr[X \ge 1] \le \mathbb E[X] \to 0。

当 p≫p(n)p \gg p(n) 时，Pr⁡[X=0]≤Pr⁡[∣X−E[X]∣≥E[X]]≤Var[X]E[X]2\Pr[X = 0] \le \Pr[|X - \mathbb E[X]| \ge \mathbb E[X]] \le \dfrac{{\rm Var}[X]}{\mathbb E[X]^2}。

由于
Var[X]=∑CVar[XC]+∑C,DCov[XC,XD]≤Θ(n4p6)+(n6)(62)p11+(n5)(53)p9=Θ(n4p6)+Θ(n6p11)+Θ(n5p9)\begin{aligned} \mathrm{Var}[X] & = \sum_{C} \mathrm{Var}[X_C] + \sum_{C, D} \mathrm{Cov}[X_C, X_D]\\ & \le \Theta(n^4p^6) + \binom n 6 \binom 6 2 p^{11} + \binom n 5 \binom 5 3 p^{9}\\ & = \Theta(n^4p^6) + \Theta(n^6 p^{11}) + \Theta(n^5p^9) \end{aligned}

从而 Var[X]E[X]2=Θ(n−4p−6)+Θ(n−2p−1)+Θ(n−3p−3)→0\dfrac{{\rm Var}[X]}{\mathbb E[X]^2} = \Theta(n^{-4}p^{-6}) + \Theta(n^{-2} p^{-1}) + \Theta(n^{-3}p^{-3}) \to 0。

该方法不适用于密集程度“不均匀”的图。